利用期望收益来评估不同的系统
注意一下这个数与我们从禅球袋子中得到的期望收益是很不相同的。原因是这并不是以“每l美元风险的期望收益”形式表示的。因此把你的期望收益化简到每!美元风险的期望的期望收益也是很重要的。表6-3表示了这个交易产生的收入和亏损的分布。把这些交易以500美元的差距分组,仅仅是因为这么做比较方便,而且500美元好像能最佳地描述最小亏损额。当你察看利润和亏损组的分布时,可能会注意到最小亏损额。有一个特定的值在这个给定的分布中,这个最小亏损额大约是500美元。现在我们在某种程度上可以把这个表看作是一个弹球袋,来注意一下期望收益。这里我们通过把大致的收入或亏损额除以大致的最小亏损额500美元计算出回报。表6-4是执行这个计算后的结果这个系统基本上能在40%的交易中赚钱,就是36/90,可以略去的交易不计算在内。系统的总利润大约是10000美元,而且全部利润都归于一次交易,那次交易可以带给你14256美元的利润。你也同样会注意到,只要除去一次亏损,就是3221美元的那次亏损,就可以增加4O%的利润。你需要仔细地研究一下这些交易。是什么产生了大笔的收入?你能预期将来会更多吗?这种收入的几率只能是1.1%,还是你能找到更好的方法?如何产生亏损的呢?是什么导致了3221美元的亏损?这个亏损的真正期望收益是1.1%,还是你预期会比它更多或更少?亏损的原因是由于心理方面的错误吗?如果是这样,以后如何来避免这些错误呢?当你从如表6-4所示的回报矩阵角度来考虑系统时,就能回答上面一大堆问题了。我们可以应用期望收益公式(6-2)来确定每1 美元风险的期望收益。这里,我们通过加和盈利交易中的正期望收益得到以下总的正期望收益期望收益公式的正数部分= 0.167*1+0.111*2+0.067*3+0.033*5+0.011*9+0.011*25算完其中的乘法后,就可以得到0.167+0.222+0.199+0.165+0.099+0.275=1.127。因此,盈利交易的总的正期望收益是1.127美元。现在需要找出亏损交易的负期望收益,如下确定每个亏损组的结果期望收益公式的负数部分=0.367*1+0.189*2+0.033*3+0.011*6=0.367+0.378+0.099+0.066=0.91 因此, 亏损交易的总的负期望收益是91美分。同样,想得到每1美元风险的总的期望收益,我们只要把总的负期望收益从总的正期望收益中减掉就行$1.127- $0.91=$0.217。因此,这个系统每1 美元风险的期望收益是21.7美分。这给了我们一个更好的对比这个系统与其他系统的基础。一个10000美元的利润可能使一个系统看上去很不错,但是知道了这个系统中每1美元风险只能产生21.7美分的期望收益后,我们就会从一个不同的角度来审视它了。6.6 利用期望收益来评估不同的系统让我们来看一下两个不同的交易系统,从而确定期望收益是如何被利用的。6.6.1 弗雷德的系统第一个系统来自于一个叫做弗雷德的期货交易商。从5月1日-8月31日,他已经完成了21次交易,如表6-5所示。这个系统在四个月的21交易中赚了1890.43美元。这相当于平均每次交易盈利90.02美元。但是该系统的每1美元风险的期望收益是多少呢?我们把这个表分解成如表6-6所示的任意美元的组合。既然弗雷德的交易中最小亏损额大约在150美元左右,那么我们就把表6-6转化成如表6-7所示的几率矩阵,把150美元当作是最小风险额。我们也同样会除去那些可以略去的交易,最后,总共就剩下18次交易。现在把公式(6-2)应用到这个矩阵来大致确定一下每1美元风险的期望收益。首先计算一下盈利交易的正期望收益。正期望收益=0.056*1+0.056*2+0.056*3+0.056*8+0.111*13+0.056*25 算完乘法后,结果是0.112+0.168+0.448+1.443+1.4=3.627(美元)接下来必须计算亏损交易产生的负期望收益。负期望收益=0.111*1+0.278*2+0.111*3+0.056*8+0.056*25计算完乘法后,结果是0.111+0.556+0.333+0.448+1.4=2.848(美元)把负期望收益从正期望收益中减掉后就得到如下的总期望收益$3.627-$2.848=$0.779。因此, 弗雷德的系统在四个月的交易期间,每1美元风险产生78美分的期望收益。记住,在这些计算中有很多四舍五入。弗雷德的系统的一个最大缺点是,它有一次巨大的25:1的亏损, 抵消了一笔25:1的盈利交易。若是没有那次亏损,弗雷德的系统会非常出色。因此,弗雷德需要研究一下那个亏损,看看类似的亏损在将来是否能避免。 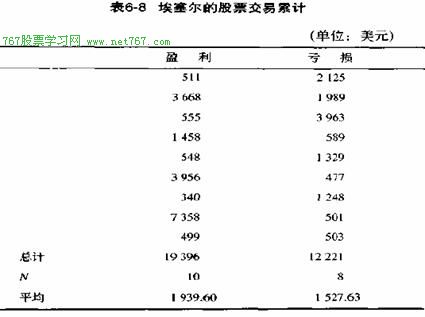

该系统在一年的18次交易中赚了7175美元。这相当于平均每次交易的盈利是398.61美元。记住弗雷德的系统每次交易只赚到90美元。此外, 埃塞尔的系统有55.6%的时间都是赚钱的,而弗雷德的系统却只有45%的时间是赚钱的。显然,埃塞尔的系统比较好。是不是这样呢?让我们看一下埃塞尔系统的每1美元风险的期望收益和机会因素。考虑进这些因素后,埃塞尔是不是仍然有一个较好的系统?表6-9显示了埃塞尔系统的各种美元组合。埃塞尔有三个最小亏损额,每个大约是500美元:一个是477美元,一个是501美元,还有一个是589美元。因此,我们假定埃塞尔的最小风险额是500美元左右。我们可以对埃塞尔的交易开发一个如表6-10所示的几率矩阵。
再次把公式(6-2)应用到表6-10的矩阵,大致确定每1美元风险的期望收益。首先,计算盈利交易的正期望收益。正期望收益=0.333*1+0.056*3+0.111*8+0.056*15算完乘法后,就可以得到如下总的正期望收益0.333+0.168+0.888+0.840=2.229(美元)现在需要计算一下亏损交易的总的负期望收益。负期望收益=0.168*1+0.111*3+0.111*4+0.056*8 算完乘法后,就可以得到如下总的负期望收益 0.168+0,333+0.444+0.448=1.393(美元) 把总的负期望收益从总的正期望收益中减掉后, 就得到$2. 229-$l.393=$0.836埃塞尔的84美分的每1美元风险期望收益要比弗雷德的78美分的风险期望收益多一些。从期望收益方面来说.埃塞尔有一个稍微好一点的系统。记住,弗雷德的利润几乎是一次好交易的函数。同样地,对埃塞尔的利润来说也是如此。她的一次7358美元的利润就要比她整年的净利润7175美元多。因此,一年中,一次交易就使她赚到了全部的利润。这对好的长期系统来说是很正常的。但是机会因素又如何发挥作用呢?弗雷德在四个月内做了18次交易,实际上要比18次还多,但是一些被略去了.因为它们的盈利或者亏损额不多于100美元,可以被忽略。两年之内,弗雷德可以进行三倍以上次交易。为了真正地评估这个系统.让我们把期望收益与几率乘起来进行比较。
3下一页当你从期望收益和几率之积这个角度来看这两个系统时,弗雷德就有一个好得多的系统。然而,这里假定两个投资者都最大化地利用了他们的机会。这两个系统的对比引起了一个与机会相关的有趣的变量。埃塞尔在一年中只进行18次交易.但这并不意味着她只有18次交易机会。只有在以下这些情形下,一个投资者才可能最大化地利用他的交易机会:(1)有交易机会时,他的资金是充足的,就是说能够进行充分的头寸调整;(2)他有一个离市策略,并且在这个策略被触发时离市;(3)在现金允许的情况下,他会充分地利用其他机会。如果这三个标准中的任何一个没有达到,通过期望收益和几率进行系统对比都是无效的。6.7对如何使用期望收益的回顾回顾一下,一旦你有了一个系统,或者至少是有了一个初步的系统.就需要计算它的期望收益,并考虑与期望收益相关的一系列问题。下面就是这些步骤。(1)计算系统的总期望收益。如果你正在使用一个系统或已经测试了一个系统,就可以计算该系统的期望收益了,只要简单地把总利润除以交易数就行。注意,到这一步为止,你仍然没有得到每1美元风险的期望收益。(2)只考虑一个单位或者100股股票,忽略头寸调整的影响效果。(3)依据最小亏损的数额大小,以100美元或500美元为范围,对交易的利润和亏损进行分组。最小亏损与你把止损点放在什么地方有关,这是系统的1R水平。这一步,你只是在评定系统的期望收益,而不是在提高它。(4)把“最小亏损额”当作单个单位,然后将交易分组转化成一个几率矩阵,找出每1美元风险的期望收益。。(5)利用公式(6-2)从几率表中计算出系统的期望收益。(6)如果你的系统至少包含有100次交易,并且每1美元风险的期望收益都在50美分之上,那么这个系统就是一个良好的系统。这只是一个好的长期系统应具备的一般标准。如果有足够多的机会,即使期望收益再低,你也会很高兴。(7)确定达到期望收益需要的机会。看一下在你的几率矩阵中确定的“弹球”的大小。通过这些弹球你能对系统有些什么了解?如何改变系统从而增加高回报盈利交易?如何改变系统从而减少高成本的亏损交易?记住以下两点:(1)盈利的期望收益和几率并不是同一样东西。人们有一种偏向,希望每次交易或者投资都是正确的。因此,他们一般都会被高几率的入市系统所吸引。然而,这些系统经常都是与大笔亏损相关联,并会导致负的期望收益。因此,要总是朝着系统期望收益的方向冒险。(2)即使是有很高的正期望收益的系统,也仍然可能导致亏损。如果你在一次交易中下的赌注太大,并且输了,那么想恢复就很困难了。3- 上一篇:第三部分 理解系统中的关键部分
- 下一篇:期望收益和R乘数

